Capítulo 7 Guía 4 - Probabilidades. Distribuciones de probabilidad.

7.1 Objetivos

Que el alumno

Calcule probabilidades.
Reconozca las gráficas de las funciones de distribución y comprendan los cambios que producen los parámetros
Obtengan probabilidades acumuladas menores o mayores a un valor y entre 2 valores.
Adquiera competencias en la aplicación de probabilidades a ejemplos reales.

7.2 Ejercicio 1

Calcular las probabilidades de obtener:

Un número impar en una sola tirada de un dado.
La presentación, como mínimo, de una “cara” en dos tiradas de una moneda.
La presentación de un as, un diez de diamante o el dos de pick en una sola extracción de u na carta de un mazo de 52.
La obtención de 7 puntos en una tirada de un par de dados.

7.3 Ejercicio 2

Una máquina produce piezas de tipo A y de tipo B. La probabilidad que una pieza A sea defectuosa es de 0.04 y la probabilidad que una pieza B lo sea es de 0.035. Calcular: * La probabilidad que las dos piezas sean defectuosas. * La probabilidad que ninguna de las dos piezas sea defectuosa.
* La probabilidad que sea defectuosa la pieza A y no la B. * La probabilidad que al menos una de las dos sea defectuosa.

7.4 Ejercicio 3

En un estudio se determinó que la probabilidad de que se produzca un artículo defectuoso en una determinada fábrica es del 0.15. Si se toman 5 artículos de ese lote al azar, y se prueban los mismos. ¿Cuál es la probabilidad?:

de que 3 o menos de 3 sean defectuosos.
de que menos de 3 sean defectuosos
de que más de 2 sean defectuosos
realizar los cálculos manualmente y verificar los resultados hallados con R.
Grafique la distribución binomial correspondiente en R. En este caso, el valor de p=0.15. ¿El sesgo es positivo o negativo? Fundamente.

7.4.1 En R

Probabilidad de que 3 sean defectuosos == P(x=2)

#Para calcular una probabilidad puntual con distribución binomial
dbinom(x=3, size=5, prob=0.15)

Probabilidad de que 3 o menos de 3 sean defectuosos == P(X<=3)

pbinom(q=2, size=5, prob=0.15, lower.tail=TRUE)

Probabilidad de que más de 2 sean defectuosos == P(X>2)

pbinom(q=2, size=5, prob=0.15, lower.tail=FALSE)

Mediante las siguientes líneas de código va a poder graficar una distribución binomial. Fundamente si el sesgo es positivo o negativo.

x <- -1:4
prob <- dbinom(x,5,0.15)
barplot(prob,col = "blue",ylim = c(0, 0.6),names.arg=x,
        main="Binomial Distribution\n(n=5,p=0.15)")

7.5 Ejercicio 4

En una localidad, en el mes de Julio se producen 2 heladas semanales (en promedio) * ¿Cuál es la probabilidad de que en 3 semanas se produzcan sólo 2 heladas? * Realizar los cálculos manualmente y verificar los resultados hallados con R.

7.5.1 En R

¿Cuál es la probabilidad de que en 3 semanas se produzcan 2 heladas?

dpois(x=2, lambda=6)

7.6 Ejercicio 5

Graficar las siguientes funciones de densidad discretas y continuas. Interpretar las diferencias observadas al cambiar los parámetros y escribir al menos 2 características de las curvas de las distribuciones que se graficaron.

N(0,1); N(0,2); N(3,1)
T(5); T(100)

7.6.1 En R

Para graficar funciones de densidad utilizamos la función curve()

par(mfrow=c(2,2)) #permite disponer gráficos de a grupos 
curve(dnorm(x, mean = 0, sd = 1), #distribución de probabilidad normal
      from = -4, #límite inferior del eje x
      to = 4, #límite superior del eje x
      type = "l", #tipo de linea trazada
      xlab = "", #sin rótulo el eje X
      ylab = "Probability Density", #rótulo eje Y
      main = "Normal Distribution") #título del gráfico
curve(dnorm(x, mean = 0, sd = 2), #distribución de probabilidad normal
      from = -6, #límite inferior del eje x
      to = 6, #límite superior del eje x
      type = "l", #tipo de linea trazada
      xlab = "", #sin rótulo el eje X
      ylab = "Probability Density", #rótulo eje Y
      main = "Normal Distribution") #título del gráfico
curve(dnorm(x, mean = 3, sd = 1), #distribución de probabilidad normal
      from = -1, #límite inferior del eje x
      to = 7, #límite superior del eje x
      type = "l", #tipo de linea trazada
      xlab = "", #sin rótulo el eje X
      ylab = "Probability Density", #rótulo eje Y
      main = "Normal Distribution") #título del gráfico

De igual manera para una distribucion t de student

par(mfrow=c(2,2)) 
curve(dt(x, df = 5),
      from = -4,
      to = 4,
      type = "l",
      lwd = 2,
      xlab = "Random Variable X",
      ylab = "Probability Density",
      main = "Student's t Distribution",
      ylim = c(0, 0.4))
abline(h = 0)
curve(dt(x, df = 100),
      from = -4,
      to = 4,
      type = "l",
      lwd = 2,
      xlab = "Random Variable X",
      ylab = "Probability Density",
      main = "Student's t Distribution",
      ylim = c(0, 0.4))
abline(h = 0)

7.6.2 Ejercicio 6

Dada una distribución normal general con x con u=5 y sigma=16. Encontrar las siguientes probabilidades:

P(x<15)
P(x<0)
P(0<x<15)
P(x>15)

Para ello puede entrar a la siguiente dirección

https://gallery.shinyapps.io/dist_calc/ y elija las siguientes opciones

Distribución normal
media = 5
desviación estándar = 16

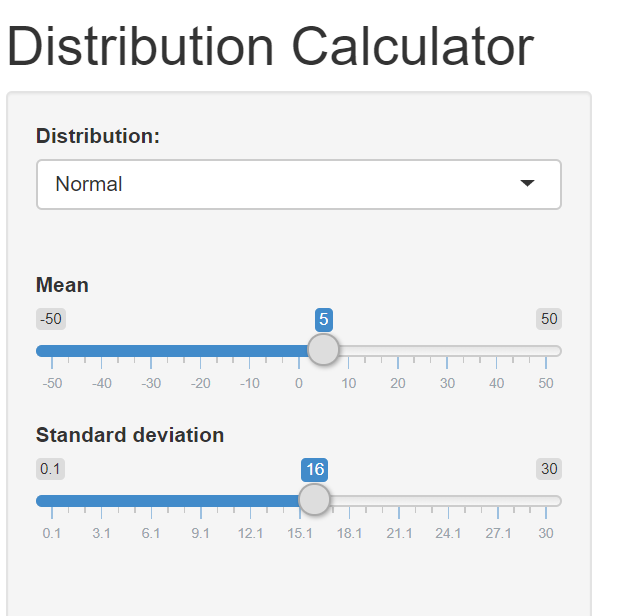
P(x<15)

P(x<0)

P(0<x<15)
P(x>15)

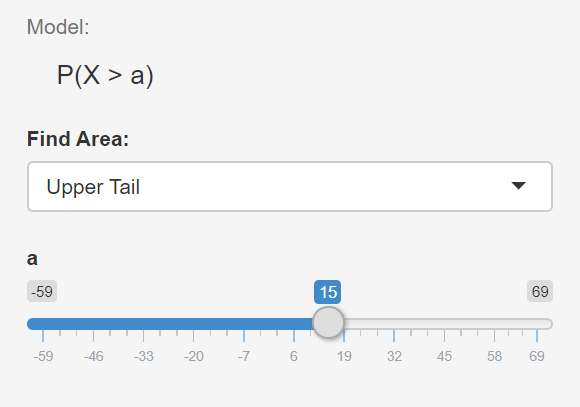
En todos los casos, observe el sombreado del área bajo la curva y anote al menos 4 oraciones describiendo los distintos casos.

7.7 Ejercicio 6

Se supone que la estancia de los enfermos en un hospital sigue una distribución normal de media 8 y desviación típica de 3. Calcular la probabilidad de que la estancia de un enfermo:

Sea inferior a 7 días.
Sea superior a 3 días.
Este comprendida entre 10 y 12 días.

Realice manualmente los ejercicios y corrobore los ejercicios mediante R.

7.7.1 En R

Sea inferior a 7 dias —> P(x<7)

pnorm(7, mean=8, sd=3)

Sea superior a 3 días —> P(x>3) = 1-P(x<3)

1-pnorm(3, mean=8, sd=3)

Este comprendida entre 10 y 12 días

dias10<-pnorm(10, 8, 3) #cálculo de área hasta el día 10
dias12<-pnorm(12, 8, 3) #cálculo de área hasta el día 12
dias12-dias10 #resto para conocer el área